Pythagorean Theorem is a widely used theorem in math and geometry with many applications. It shows the relationship of the 3 sides of a right triangle. It is used so much, that it is hard to not know it. However, many students just know it as it is. They never know how to prove it. How do you know Pythagorean Theorem formula is true? Today we are going to show you, with the toy you have at home, LEGO. Created by my son, this is the easiest proof of Pythagorean Theorem, so easy that a 3rd grader will be able to do it. Sometimes kids have better ideas, and this is one of them.
To prove Pythagorean Theorem following the strict mathematics method, some one needs understand many advanced math concepts first, such as square root. For elementary students who have no knowledge of these concepts, it is hard to understand the mathematic proof of the theorem. However, many schools instroduce Pythagorean Theorem at elementary school level. To avoiding confusing kids, it goes without a proof. It is just introduce as it is. As kids see it again in middle and high school, they are not shown the proof, because they “already know it well”. This leads to the void in students’ math path through high school that it is never be proved.
With this method of Pythagorean Theorem proof with LEGO, kids don’t need many advanced knowledge. All they need know is the area of a square, which is the product of the two sides. Since the two sides are the same length for the square shape, it is square of the sides. If kids don’t have the concept of square yet, you can just stop at the concept of the product of the two sides.
Pythagorean Theorem Definition

To understand why the proof works, let’s first look at the Pythagorean Theorem: a² + b² = c²
As show in the equation, Pythagorean Theorem is about the relationship among the 3 sides of a right triangle. If a and b are the lengths of the legs of a right triangle and c is the length of the hypotenuse, the side opposite to the right angle, then the sum of the squares of the lengths of the legs (a² + b²) or (a x a + b x b) is equal to the square of the length of the hypotenuse c² or (c x c).
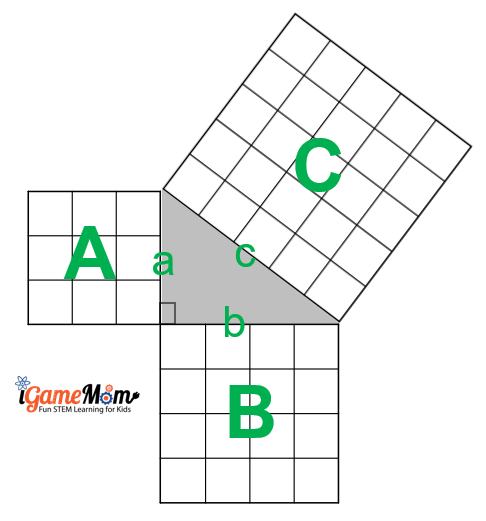
With this, we can see that a² is the area of a square A with all sides length being a, and b² is the area of a square B with the side length as b, and c² is the area of a square C of the side length c. To prove the Pythagorean Theorem, we just need prove the sum of the areas of square A and square B is equal to the area of square C.
Now, with LEGO, we can make 3 squares that the length of their sides satisfy a² + b² = c².
How do we find these squares?
Find Pathagorean Triples
Luckily, there are so many research on Pythagorean Theorem, a quick search on Google can give us many of these square triples. To save your time, I have listed out all 16 primitive Pythagorean Triples under 100. Yes, there are just 16 primitive triples under 100. You can download the list, together with a LEGO proof template at the bottom of this post. I will explain about the template shortly.
Primitive means the 3 numbers don’t share common factors greater than 1. An example is (3, 4, 5).
You may ask, how about (6, 8, 10)? Or (9, 12, 15)?
They are also Pythagorean triples. But they are not primitive triples, since they are multiple of (3, 4, 5).
Now you know, besides the primitive triples, there are many more Pythagorean triples. For example, based on the 2nd triple on our list (5, 12, 13), you know (10, 24, 26) is also a Pythagorean Triple.
Move on to the proof.
Prove Pythagorean Theorem with LEGO
These are the steps to prove Pythagorean Theorem with LEGO:
What do you find?
You see the big square is completely covered by the 1×1 LEGO pieces, and no LEGO 1×1 pieces is left on the two smaller squares.
What is the conclusion of this activity?
The conclusion is the sum of the areas of the two smaller squares equals the area of the biggest square, ie., a² + b² = c²
Now, you just proved the Pythagorean Theorem with LEGO!

Looking for more LEGO math activities? Try LEGO Math to Learn COordinate Plane and LEGO Movie Math for Areas and Perimeters.

 .
.




